Kvadratisk ligning modulo hvordan løses. Hvordan løse likninger med modul

Et av de vanskeligste temaene for studenter er å løse ligninger som inneholder en variabel under modultegnet. La oss først finne ut hva dette henger sammen med? Hvorfor, for eksempel, knekker de fleste barn andregradsligninger som nøtter, men har så mange problemer med et så langt fra komplekst konsept som en modul?

Etter min mening er alle disse vanskelighetene forbundet med mangelen på klart formulerte regler for å løse likninger med en modul. Så, bestemmer kvadratisk ligning, vet eleven med sikkerhet at han først må bruke diskriminantformelen, og deretter formlene for røttene til kvadratisk ligning. Hva gjør jeg hvis en modul finnes i ligningen? Vi vil prøve å beskrive tydelig nødvendig plan handlinger i tilfellet når ligningen inneholder en ukjent under modultegnet. Vi vil gi flere eksempler for hvert tilfelle.

Men først, la oss huske moduldefinisjon. Så modulo tallet en dette nummeret i seg selv kalles if en ikke-negativ og -en, hvis nummer en mindre enn null. Du kan skrive det slik:

|a| = a hvis a ≥ 0 og |a| = -a hvis a< 0

Når vi snakker om den geometriske betydningen av modulen, bør det huskes at hvert reelt tall tilsvarer et bestemt punkt på tallaksen - dens koordinere. Så modulen eller absoluttverdien til et tall er avstanden fra dette punktet til opprinnelsen til den numeriske aksen. Avstanden er alltid spesifisert positivt tall. Dermed modulen til evt negativt tall er et positivt tall. Forresten, selv på dette stadiet begynner mange studenter å bli forvirret. Modulen kan inneholde et hvilket som helst tall, men resultatet av bruk av modulen er alltid et positivt tall.

La oss nå gå direkte til å løse likningene.

1. Tenk på en ligning på formen |x| = c, hvor c er et reelt tall. Denne ligningen kan løses ved å bruke moduldefinisjonen.

Vi deler alle reelle tall i tre grupper: de som er større enn null, de som er mindre enn null, og den tredje gruppen er tallet 0. Vi skriver løsningen i form av et diagram:

(±c, hvis c > 0

Hvis |x| = c, så x = (0, hvis c = 0

(ingen røtter hvis med< 0

1) |x| = 5, fordi 5 > 0, så x = ±5;

2) |x| = -5, fordi -5< 0, то уравнение не имеет корней;

3) |x| = 0, deretter x = 0.

2. Ligning av formen |f(x)| = b, hvor b > 0. For å løse denne ligningen er det nødvendig å kvitte seg med modulen. Vi gjør det på denne måten: f(x) = b eller f(x) = -b. Nå må du løse hver av de resulterende ligningene separat. Hvis i den opprinnelige ligningen b< 0, решений не будет.

1) |x + 2| = 4, fordi 4 > 0, da

x + 2 = 4 eller x + 2 = -4

2) |x 2 – 5| = 11, fordi 11 > 0, da

x 2 – 5 = 11 eller x 2 – 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 ingen røtter

3) |x 2 – 5x| = -8, fordi -8< 0, то уравнение не имеет корней.

3. En ligning på formen |f(x)| = g(x). I henhold til betydningen av modulen vil en slik ligning ha løsninger hvis dens høyre side er større enn eller lik null, dvs. g(x) ≥ 0. Da vil vi ha:

f(x) = g(x) eller f(x) = -g(x).

1) |2x – 1| = 5x – 10. Denne ligningen vil ha røtter hvis 5x – 10 ≥ 0. Det er her løsningen av slike ligninger begynner.

1. O.D.Z. 5x – 10 ≥ 0

2. Løsning:

2x – 1 = 5x – 10 eller 2x – 1 = -(5x – 10)

3. Vi kombinerer O.D.Z. og løsningen får vi:

Roten x = 11/7 passer ikke til O.D.Z., den er mindre enn 2, men x = 3 tilfredsstiller denne betingelsen.

Svar: x = 3

2) |x – 1| = 1 – x 2.

1. O.D.Z. 1 – x 2 ≥ 0. La oss løse denne ulikheten ved å bruke intervallmetoden:

(1 – x)(1 + x) ≥ 0

2. Løsning:

x – 1 = 1 – x 2 eller x – 1 = -(1 – x 2)

x 2 + x – 2 = 0 x 2 – x = 0

x = -2 eller x = 1 x = 0 eller x = 1

3. Vi kombinerer løsningen og O.D.Z.:

Bare røttene x = 1 og x = 0 er egnet.

Svar: x = 0, x = 1.

4. Ligning av formen |f(x)| = |g(x)|. En slik likning er ekvivalent med de følgende to likningene f(x) = g(x) eller f(x) = -g(x).

1) |x 2 – 5x + 7| = |2x – 5|. Denne ligningen tilsvarer de to følgende:

x 2 – 5x + 7 = 2x – 5 eller x 2 – 5x +7 = -2x + 5

x 2 – 7x + 12 = 0 x 2 – 3x + 2 = 0

x = 3 eller x = 4 x = 2 eller x = 1

Svar: x = 1, x = 2, x = 3, x = 4.

5. Ligninger løst ved substitusjonsmetoden (variabel erstatning). Denne løsningsmetoden er enklest forklart i spesifikt eksempel. Så la oss få en andregradsligning med modul:

x 2 – 6|x| + 5 = 0. Ved modulegenskapen x 2 = |x| 2, så ligningen kan skrives om som følger:

|x| 2 – 6|x| + 5 = 0. La oss erstatte |x| = t ≥ 0, da vil vi ha:

t 2 – 6t + 5 = 0. Ved å løse denne ligningen finner vi at t = 1 eller t = 5. La oss gå tilbake til erstatningen:

|x| = 1 eller |x| = 5

x = ±1 x = ±5

Svar: x = -5, x = -1, x = 1, x = 5.

La oss se på et annet eksempel:

x 2 + |x| – 2 = 0. Ved modulegenskapen x 2 = |x| 2, derfor

|x| 2 + |x| – 2 = 0. La oss erstatte |x| = t ≥ 0, deretter:

t 2 + t – 2 = 0. Ved å løse denne ligningen får vi t = -2 eller t = 1. La oss gå tilbake til erstatningen:

|x| = -2 eller |x| = 1

Ingen røtter x = ± 1

Svar: x = -1, x = 1.

6. En annen type ligninger er ligninger med en "kompleks" modul. Slike ligninger inkluderer ligninger som har "moduler i en modul." Ligninger av denne typen kan løses ved hjelp av egenskapene til modulen.

1) |3 – |x|| = 4. Vi vil handle på samme måte som i ligninger av den andre typen. Fordi 4 > 0, så får vi to ligninger:

3 – |x| = 4 eller 3 – |x| = -4.

La oss nå uttrykke modulen x i hver ligning, deretter |x| = -1 eller |x| = 7.

Vi løser hver av de resulterende ligningene. Det er ingen røtter i den første ligningen, fordi -1< 0, а во втором x = ±7.

Svar x = -7, x = 7.

2) |3 + |x + 1|| = 5. Vi løser denne ligningen på lignende måte:

3 + |x + 1| = 5 eller 3 + |x + 1| = -5

|x + 1| = 2 |x + 1| = -8

x + 1 = 2 eller x + 1 = -2. Ingen røtter.

Svar: x = -3, x = 1.

Det er også universell metode løse likninger med modul. Dette er intervallmetoden. Men vi skal se på det senere.

nettside, ved kopiering av materiale helt eller delvis, kreves en lenke til kilden.

Blant eksempler per modul Ofte er det ligninger du må finne modulrøtter i en modul, det vil si en formlikning
||a*x-b|-c|=k*x+m .
Hvis k=0, det vil si at høyresiden er lik en konstant (m), så er det lettere å se etter en løsning ligninger med moduler grafisk. Nedenfor er metoden åpning av doble moduler ved å bruke eksempler som er vanlige i praksis. Forstå algoritmen for å regne ut ligninger med moduler godt, for ikke å få problemer på tester, tester og bare for å vite.

Eksempel 1. Løs ligningen modulo |3|x|-5|=-2x-2.
Løsning: Begynn alltid å åpne ligninger fra den interne modulen
|x|=0 <->x=0.
Ved punktet x=0 deles ligningen med modul på 2.
På x< 0 подмодульная функция отрицательная, поэтому при раскрытии знак меняем на противоположный
|-3x-5|=-2x-2.
For x>0 eller lik, utvidelse av modulen får vi
|3x-5|=-2x-2 .
La oss løse ligningen for negative variabler (x< 0) . Оно разлагается на две системы уравнений. Первое уравнение получаем из условия, что функция после знака равенства неотрицательна. Второе - раскрывая модуль в одной системе принимаем, что подмодульная функция положительная, в иной отрицательная - меняем знак правой или левой части (зависит от методики преподавания).

Fra den første ligningen får vi at løsningen ikke skal overstige (-1), dvs.

Denne begrensningen tilhører helt og holdent området vi løser. La oss flytte variabler og konstanter på tvers forskjellige sider likestilling i første og andre system

og finne en løsning

Begge verdiene tilhører intervallet som vurderes, det vil si at de er røtter.
Tenk på en ligning med moduler for positive variabler
|3x-5|=-2x-2.
Ved å utvide modulen får vi to ligningssystemer

Fra den første ligningen, som er felles for de to systemene, får vi den kjente tilstanden

som, i skjæringspunktet med settet vi leter etter en løsning på, gir et tomt sett (det er ingen skjæringspunkter). Så de eneste røttene til en modul med en modul er verdiene
x=-3; x=-1,4.

Eksempel 2. Løs ligningen med modul ||x-1|-2|=3x-4.
Løsning: La oss starte med å åpne den interne modulen
|x-1|=0 <=>x=1.
En submodulær funksjon endrer fortegn ved ett. For mindre verdier er det negativt, for større verdier er det positivt. I samsvar med dette, når vi utvider den interne modulen, får vi to ligninger med modulen
x |-(x-1)-2|=3x-4;
x>=1 -> |x-1-2|=3x-4.
Sørg for å sjekke høyre side av modulligningen den må være større enn null.
3x-4>=0 -> x>=4/3.
Dette betyr at det ikke er nødvendig å løse den første ligningen, siden den ble skrevet for x< 1, что не соответствует найденному условию. Раскроем модуль во втором уравнении
|x-3|=3x-4 ->
x-3=3x-4 eller x-3=4-3x;
4-3=3x-x eller x+3x=4+3;
2x=1 eller 4x=7;
x=1/2 eller x=7/4.
Vi mottok to verdier, hvorav den første blir avvist fordi den ikke tilhører det nødvendige intervallet. Til slutt har ligningen én løsning x=7/4.

Eksempel 3. Løs ligningen med modul ||2x-5|-1|=x+3.
Løsning: La oss åpne den interne modulen
|2x-5|=0 <=>x=5/2=2,5.
Punktet x=2,5 deler talllinjen i to intervaller. Henholdsvis submodulær funksjon skifter fortegn ved passering gjennom 2.5. La oss skrive ned betingelsen for løsningen med høyre side ligninger med modul.
x+3>=0 -> x>=-3.
Så løsningen kan være verdier ikke mindre enn (-3) . La oss utvide modulen for negativ verdi innendørs modul
|-(2x-5)-1|=x+3;
|-2x+4|=x+3.
Denne modulen vil også gi 2 ligninger når den utvides
-2x+4=x+3 eller 2x-4=x+3;
2x+x=4-3 eller 2x-x=3+4;
3x=1; x=1/3 eller x=7 .
Vi avviser verdien x=7, siden vi lette etter en løsning i intervallet [-3;2.5]. Nå åpner vi den interne modulen for x>2.5. Vi får en ligning med én modul
|2x-5-1|=x+3;
|2x-6|=x+3.
Ved utvidelse av modulen får vi følgende lineære ligninger
-2x+6=x+3 eller 2x-6=x+3;
2x+x=6-3 eller 2x-x=3+6;
3x=3; x=1 eller x=9 .
Den første verdien x=1 tilfredsstiller ikke betingelsen x>2,5. Så på dette intervallet har vi én rot av ligningen med modul x=9, og det er to totalt (x=1/3) Ved substitusjon kan du sjekke riktigheten av beregningene som er utført
Svar: x=1/3; x=9.

Eksempel 4. Finn løsninger på dobbelmodulen ||3x-1|-5|=2x-3.
Løsning: La oss utvide den interne modulen til ligningen
|3x-1|=0 <=>x=1/3.
Punktet x=2,5 deler talllinjen i to intervaller, og gitt ligning for to saker. Vi skriver ned betingelsen for løsningen basert på formen til ligningen på høyre side
2x-3>=0 -> x>=3/2=1,5.
Det følger at vi er interessert i verdier>=1,5. Dermed modulær ligning vurdere på to intervaller
,
|-(3x-1)-5|=2x-3;
|-3x-4|=2x-3.
Den resulterende modulen, når den utvides, er delt inn i 2 ligninger
-3x-4=2x-3 eller 3x+4=2x-3;
2x+3x=-4+3 eller 3x-2x=-3-4;
5x=-1; x=-1/5 eller x=-7 .
Begge verdiene faller ikke inn i intervallet, det vil si at de ikke er løsninger på ligningen med moduler. Deretter utvider vi modulen for x>2.5. Vi får følgende ligning
|3x-1-5|=2x-3;
|3x-6|=2x-3.
Ved å utvide modulen får vi 2 lineære ligninger
3x-6=2x-3 eller –(3x-6)=2x-3;
3x-2x=-3+6 eller 2x+3x=6+3;
x=3 eller 5x=9; x=9/5=1,8.
Den andre verdien som ble funnet samsvarer ikke med betingelsen x>2.5, vi avviser den.
Til slutt har vi én rot av ligningen med modul x=3.
Utfører en sjekk
||3*3-1|-5|=2*3-3 3=3 .
Roten av ligningen med modulen ble beregnet riktig.
Svar: x=1/3; x=9.

Å opprettholde personvernet ditt er viktig for oss. Av denne grunn har vi utviklet en personvernerklæring som beskriver hvordan vi bruker og lagrer informasjonen din. Se gjennom vår personvernpraksis og gi oss beskjed hvis du har spørsmål.

Innsamling og bruk av personopplysninger

Personopplysninger refererer til data som kan brukes til å identifisere eller kontakte en bestemt person.

Du kan bli bedt om å oppgi din personlige informasjon når som helst når du kontakter oss.

Nedenfor er noen eksempler på hvilke typer personopplysninger vi kan samle inn og hvordan vi kan bruke slik informasjon.

Hvilken personlig informasjon samler vi inn:

Når du sender inn en forespørsel på nettstedet, kan vi samle inn ulike opplysninger, inkludert navn, telefonnummer, adresse E-post etc.

Hvordan vi bruker dine personopplysninger:

Personopplysningene vi samler inn gjør at vi kan kontakte deg og informere deg om unike tilbud, kampanjer og andre arrangementer og kommende arrangementer.
Fra tid til annen kan vi bruke din personlige informasjon til å sende viktige meldinger og kommunikasjoner.
Vi kan også bruke personopplysninger til interne formål, som å gjennomføre revisjoner, dataanalyser og ulike undersøkelser for å forbedre tjenestene vi leverer og gi deg anbefalinger angående våre tjenester.
Hvis du deltar i en premietrekning, konkurranse eller lignende kampanje, kan vi bruke informasjonen du gir til å administrere slike programmer.

Utlevering av informasjon til tredjeparter

Vi utleverer ikke informasjonen mottatt fra deg til tredjeparter.

Unntak:

Om nødvendig - i samsvar med loven, rettslig prosedyre, rettslige prosesser og/eller basert på offentlige forespørsler eller forespørsler fra offentlige etater på den russiske føderasjonens territorium - oppgi din personlige informasjon. Vi kan også avsløre informasjon om deg hvis vi fastslår at slik avsløring er nødvendig eller hensiktsmessig for sikkerhet, rettshåndhevelse eller andre offentlige viktige formål.
I tilfelle en omorganisering, fusjon eller salg, kan vi overføre personopplysningene vi samler inn til gjeldende etterfølger tredjepart.

Beskyttelse av personopplysninger

Vi tar forholdsregler - inkludert administrative, tekniske og fysiske - for å beskytte din personlige informasjon mot tap, tyveri og misbruk, samt uautorisert tilgang, avsløring, endring og ødeleggelse.

Respekter ditt privatliv på bedriftsnivå

For å sikre at din personlige informasjon er sikker, kommuniserer vi personvern- og sikkerhetsstandarder til våre ansatte og håndhever strengt personvernpraksis.

Etter min mening er alle disse vanskelighetene forbundet med mangelen på klart formulerte regler for å løse likninger med en modul. Så når han løser en kvadratisk ligning, vet eleven med sikkerhet at han først må bruke diskriminantformelen, og deretter formlene for røttene til kvadratisk ligning. Hva gjør jeg hvis en modul finnes i ligningen? Vi vil forsøke å tydelig beskrive nødvendig handlingsplan for tilfellet når ligningen inneholder en ukjent under modultegnet. Vi vil gi flere eksempler for hvert tilfelle.

Men først, la oss huske moduldefinisjon. Så modulo tallet en dette nummeret i seg selv kalles if en ikke-negativ og -en, hvis nummer en mindre enn null. Du kan skrive det slik:

|a| = a hvis a ≥ 0 og |a| = -a hvis a< 0

Når vi snakker om den geometriske betydningen av modulen, bør det huskes at hvert reelt tall tilsvarer et bestemt punkt på tallaksen - dens koordinere. Så modulen eller absoluttverdien til et tall er avstanden fra dette punktet til opprinnelsen til den numeriske aksen. Avstanden angis alltid som et positivt tall. Dermed er modulen til ethvert negativt tall et positivt tall. Forresten, selv på dette stadiet begynner mange studenter å bli forvirret. Modulen kan inneholde et hvilket som helst tall, men resultatet av bruk av modulen er alltid et positivt tall.

La oss nå gå direkte til å løse likningene.

1. Tenk på en ligning på formen |x| = c, hvor c er et reelt tall. Denne ligningen kan løses ved å bruke moduldefinisjonen.

Vi deler alle reelle tall i tre grupper: de som er større enn null, de som er mindre enn null, og den tredje gruppen er tallet 0. Vi skriver løsningen i form av et diagram:

(±c, hvis c > 0

Hvis |x| = c, så x = (0, hvis c = 0

(ingen røtter hvis med< 0

1) |x| = 5, fordi 5 > 0, så x = ±5;

2) |x| = -5, fordi -5< 0, то уравнение не имеет корней;

3) |x| = 0, deretter x = 0.

1) |x + 2| = 4, fordi 4 > 0, da

x + 2 = 4 eller x + 2 = -4

2) |x 2 – 5| = 11, fordi 11 > 0, da

x 2 – 5 = 11 eller x 2 – 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 ingen røtter

3) |x 2 – 5x| = -8, fordi -8< 0, то уравнение не имеет корней.

3. En ligning på formen |f(x)| = g(x). I henhold til betydningen av modulen vil en slik ligning ha løsninger hvis dens høyre side er større enn eller lik null, dvs. g(x) ≥ 0. Da vil vi ha:

f(x) = g(x) eller f(x) = -g(x).

1) |2x – 1| = 5x – 10. Denne ligningen vil ha røtter hvis 5x – 10 ≥ 0. Det er her løsningen av slike ligninger begynner.

1. O.D.Z. 5x – 10 ≥ 0

2. Løsning:

2x – 1 = 5x – 10 eller 2x – 1 = -(5x – 10)

3. Vi kombinerer O.D.Z. og løsningen får vi:

Roten x = 11/7 passer ikke til O.D.Z., den er mindre enn 2, men x = 3 tilfredsstiller denne betingelsen.

Svar: x = 3

2) |x – 1| = 1 – x 2.

1. O.D.Z. 1 – x 2 ≥ 0. La oss løse denne ulikheten ved å bruke intervallmetoden:

(1 – x)(1 + x) ≥ 0

2. Løsning:

x – 1 = 1 – x 2 eller x – 1 = -(1 – x 2)

x 2 + x – 2 = 0 x 2 – x = 0

x = -2 eller x = 1 x = 0 eller x = 1

3. Vi kombinerer løsningen og O.D.Z.:

Bare røttene x = 1 og x = 0 er egnet.

Svar: x = 0, x = 1.

4. Ligning av formen |f(x)| = |g(x)|. En slik likning er ekvivalent med de følgende to likningene f(x) = g(x) eller f(x) = -g(x).

1) |x 2 – 5x + 7| = |2x – 5|. Denne ligningen tilsvarer de to følgende:

x 2 – 5x + 7 = 2x – 5 eller x 2 – 5x +7 = -2x + 5

x 2 – 7x + 12 = 0 x 2 – 3x + 2 = 0

x = 3 eller x = 4 x = 2 eller x = 1

Svar: x = 1, x = 2, x = 3, x = 4.

5. Ligninger løst ved substitusjonsmetoden (variabel erstatning). Denne løsningsmetoden er enklest å forklare med et spesifikt eksempel. Så la oss få en andregradsligning med modul:

x 2 – 6|x| + 5 = 0. Ved modulegenskapen x 2 = |x| 2, så ligningen kan skrives om som følger:

|x| 2 – 6|x| + 5 = 0. La oss erstatte |x| = t ≥ 0, da vil vi ha:

t 2 – 6t + 5 = 0. Ved å løse denne ligningen finner vi at t = 1 eller t = 5. La oss gå tilbake til erstatningen:

|x| = 1 eller |x| = 5

x = ±1 x = ±5

Svar: x = -5, x = -1, x = 1, x = 5.

La oss se på et annet eksempel:

x 2 + |x| – 2 = 0. Ved modulegenskapen x 2 = |x| 2, derfor

|x| 2 + |x| – 2 = 0. La oss erstatte |x| = t ≥ 0, deretter:

t 2 + t – 2 = 0. Ved å løse denne ligningen får vi t = -2 eller t = 1. La oss gå tilbake til erstatningen:

|x| = -2 eller |x| = 1

Ingen røtter x = ± 1

Svar: x = -1, x = 1.

1) |3 – |x|| = 4. Vi vil handle på samme måte som i ligninger av den andre typen. Fordi 4 > 0, så får vi to ligninger:

3 – |x| = 4 eller 3 – |x| = -4.

La oss nå uttrykke modulen x i hver ligning, deretter |x| = -1 eller |x| = 7.

Vi løser hver av de resulterende ligningene. Det er ingen røtter i den første ligningen, fordi -1< 0, а во втором x = ±7.

Svar x = -7, x = 7.

2) |3 + |x + 1|| = 5. Vi løser denne ligningen på lignende måte:

3 + |x + 1| = 5 eller 3 + |x + 1| = -5

|x + 1| = 2 |x + 1| = -8

x + 1 = 2 eller x + 1 = -2. Ingen røtter.

Svar: x = -3, x = 1.

Det finnes også en universell metode for å løse likninger med en modul. Dette er intervallmetoden. Men vi skal se på det senere.

blog.site, når du kopierer materiale helt eller delvis, kreves en lenke til originalkilden.

MBOU ungdomsskole nr. 17, Ivanovo

« Ligninger med modul"
Metodeutvikling

Kompilert

matte lærer

Lebedeva N.V.

20010

Forklarende merknad

Kapittel 1 Introduksjon

Seksjon 2. Grunnleggende egenskaper Seksjon 3. Geometrisk tolkning av begrepet modul til et tall Seksjon 4. Graf for funksjonen y = |x| Seksjon 5. Konvensjoner

Kapittel 2. Løse ligninger som inneholder en modul

Del 1. Ligninger av formen |F(x)| = m (enkleste) Seksjon 2. Ligninger av formen F(|x|) = m Seksjon 3. Ligninger av formen |F(x)| = G(x) Seksjon 4. Ligninger av formen |F(x)| = ± F(x) (vakreste) Seksjon 5. Ligninger av formen |F(x)| = |G(x)| Del 6. Eksempler på løsning av ikke-standardiserte ligninger Seksjon 7. Ligninger av formen |F(x)| + |G(x)| = 0 Seksjon 8. Ligninger av formen |a 1 x ± b 1 | ± |a 2 x ± b 2 | ± …|a n x ± i n | = m Seksjon 9. Ligninger som inneholder flere moduler

Kapittel 3. Eksempler på løsning av ulike ligninger med modul.

Del 1. Trigonometriske ligninger Seksjon 2. Eksponentialligninger Del 3. Logaritmiske ligninger Seksjon 4. Irrasjonelle ligninger Seksjon 5. Avanserte oppgaver Svar på øvelsene Bibliografi

Forklarende merknad.

Konseptet med absolutt verdi (modul) til et reelt tall er en av dets essensielle egenskaper. Dette konseptet er utbredt i ulike deler av fysiske, matematiske og tekniske vitenskaper. I praksis med å undervise i matematikkkurs i videregående skole i samsvar med programmet til Forsvarsdepartementet i Den russiske føderasjonen vises begrepet "absolutt verdi av et tall" gjentatte ganger: i 6. klasse introduseres definisjonen av en modul, dens geometrisk betydning; i 8. klasse dannes konseptet absolutt feil, løsningen av de enkleste ligningene og ulikhetene som inneholder en modul vurderes, egenskapene til aritmetikk studeres kvadratrot; i 11. klasse finner du konseptet i avsnittet «Root n-te grad." Undervisningserfaring viser at elevene ofte møter vanskeligheter med å løse oppgaver som krever kunnskap om dette stoffet, og ofte hopper over dem uten å begynne å fullføre dem. Tekstene til eksamensoppgaver for 9. og 11. trinn omfatter også tilsvarende oppgaver. I tillegg er kravene som universiteter stiller til skolekandidater forskjellige, nemlig mer høy level enn kravene i skolens læreplan. For livet i Moderne samfunn Det er veldig viktig å utvikle en matematisk tenkestil, som manifesterer seg i visse mentale ferdigheter. I prosessen med å løse problemer med moduler kreves evnen til å bruke teknikker som generalisering og spesifikasjon, analyse, klassifisering og systematisering og analogi. Å løse slike oppgaver lar deg teste kunnskapen din om hoveddelene av skolekurset, nivået logisk tenkning, innledende forskningsferdigheter. denne jobben er viet en av delene - løsning av ligninger som inneholder en modul. Den består av tre kapitler. Det første kapittelet introduserer grunnleggende begreper og de viktigste teoretiske betraktningene. Det andre kapittelet foreslår ni hovedtyper av ligninger som inneholder en modul, diskuterer metoder for å løse dem og undersøker eksempler ulike nivåer vanskeligheter. Det tredje kapittelet tilbyr mer komplekse og ikke-standardiserte ligninger (trigonometriske, eksponentielle, logaritmiske og irrasjonelle). For hver type ligning er det øvelser for uavhengig avgjørelse(svar og veiledning er vedlagt). Hovedformålet med dette arbeidet er å gi metodisk bistand til lærere med forberedelse til undervisning og tilrettelegging av valgfag. Materialet kan også brukes som læremiddel for videregående elever. Oppgavene som er foreslått i arbeidet er interessante og ikke alltid enkle å løse, noe som lar deg gjøre læringsmotivasjon studenter til å bli mer bevisste, teste sine evner og forbedre forberedelsesnivået til skolekandidater for å gå inn på universiteter. Et differensiert utvalg av de foreslåtte øvelsene innebærer en overgang fra det reproduktive nivået for å mestre materialet til det kreative, samt muligheten til å lære hvordan du bruker kunnskapen din når du løser ikke-standardiserte problemer.

Kapittel 1 Introduksjon.

§ 1. Fastsettelse av absolutt verdi .

Definisjon : Den absolutte verdien (modulen) til et reelt tall EN et ikke-negativt tall kalles: EN eller -EN. Betegnelse: │ EN │ Oppføringen lyder som følger: "modul av tallet a" eller "absolutt verdi av tallet a"

│ a, hvis a > 0

│a│ = │ 0, hvis a = 0 (1)

│ - og hvis a
Eksempler: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1
Utvid uttrykksmodulen:
a) │x - 8│, hvis x > 12 b) │2x + 3│, hvis x ≤ -2 │x – 8│= x – 8 │ 2x + 3│= - 2x – 3
Seksjon 2. Grunnleggende egenskaper.
La oss vurdere de grunnleggende egenskapene til absolutt verdi. Eiendom #1: Motsatte tall har like moduler, dvs. │а│=│- а│ La oss vise at likheten er riktig. La oss skrive ned definisjonen av tallet - A : │- a│= (2) La oss sammenligne sett (1) og (2). Tydeligvis definisjonene av de absolutte verdiene av tall EN Og - A matche opp. Derfor, │а│=│- а│
Når vi vurderer følgende egenskaper, vil vi begrense oss til deres formulering, siden deres bevis er gitt inn Eiendom #2: Absoluttverdien av summen av et endelig antall reelle tall overskrider ikke summen av absoluttverdiene til leddene: │а 1 + а 2 +...+ а n │ ≤│а 1 │+│а 2 │ + … + │а n │ Eiendom #3: Den absolutte verdien av differansen mellom to reelle tall overstiger ikke summen av deres absolutte verdier: │а - в│ ≤│а│+│в│ Eiendom #4: Den absolutte verdien av produktet av et endelig antall reelle tall er lik produktet av de absolutte verdiene av faktorene: │а·в│=│а│·│в│ Eiendom #5: Den absolutte verdien av kvotienten av reelle tall er lik kvotienten av deres absolutte verdier:

Seksjon 3. Geometrisk tolkning av begrepet modul til et tall.

Hvert reelt tall kan assosieres med et punkt på tallinjen, som vil være et geometrisk bilde av dette reelle tallet. Hvert punkt på tallinjen tilsvarer dets avstand fra origo, dvs. lengden på segmentet fra origo til et gitt punkt. Denne avstanden anses alltid som en ikke-negativ verdi. Derfor vil lengden på det tilsvarende segmentet være den geometriske tolkningen av den absolutte verdien av et gitt reelt tall

Den presenterte geometriske illustrasjonen bekrefter tydelig eiendom nr. 1, dvs. moduler motsatte tall er like. Herfra er gyldigheten av likheten lett å forstå: │х – а│= │а – x│. Løsningen på ligningen │х│= m, hvor m ≥ 0, nemlig x 1,2 = ± m, blir også mer åpenbar. Eksempler: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1

x 1,2 = 2; 4

Seksjon 4. Graf for funksjonen y = │х│

Domenet til denne funksjonen er alle reelle tall.

Seksjon 5. Konvensjoner.

I fremtiden, når vi vurderer eksempler på å løse ligninger, vil følgende bli brukt symboler: ( - tegn på systemet [ - tegn på helheten Når man løser et likningssystem (ulikheter), finner man skjæringspunktet mellom løsningene til likningene (ulikhetene) som inngår i systemet. Når man løser et sett med ligninger (ulikheter), finner man foreningen av løsninger som er inkludert i settet med ligninger (ulikheter).

Kapittel 2. Løse ligninger som inneholder en modul.

I dette kapittelet skal vi se på algebraiske metoder for å løse likninger som inneholder en eller flere moduler.

Del 1. Ligninger på formen │F (x)│= m

En ligning av denne typen kalles den enkleste. Den har en løsning hvis og bare hvis m ≥ 0. Per definisjon av modulen er den opprinnelige ligningen ekvivalent med et sett med to ligninger: │ F(x)│=m

Eksempler:
№1. Løs ligningen: │7х - 2│= 9

Svar: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 +3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Svar: summen av røttene er -2.№3
│x 4 -5x 2 + 2│= 2 x 4 – 5x 2 = 0 x 4 – 5x 2 + 4 = 0 x 2 (x 2 – 5) = 0 la oss betegne x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 – begge verdiene tilfredsstiller betingelsen m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Svar: antall røtter til ligning 7. Øvelser:
№1. Løs ligningen og angi summen av røttene: │х - 5│= 3 №2 . Løs ligningen og angi den minste roten: │x 2 + x│= 0 №3 . Løs ligningen og angi den største roten: │x 2 – 5x + 4│= 4 №4 .Løs ligningen og angi hele roten: │2x 2 – 7x + 6│= 1 №5 .Løs ligningen og angi antall røtter: │x 4 – 13x 2 + 50│= 14

Del 2. Ligninger av formen F(│х│) = m

Funksjonsargumentet på venstre side er under modultegnet, og høyre side er uavhengig av variabelen. La oss vurdere to måter å løse ligninger av denne typen. 1 vei: Per definisjon av absolutt verdi er den opprinnelige ligningen ekvivalent med kombinasjonen av to systemer. I hver av disse er en betingelse pålagt et submodulært uttrykk. F(│х│) =m

Siden funksjonen F(│x│) er jevn gjennom hele definisjonsdomenet, er røttene til ligningene F(x) = m og F(- x) = m par med motsatte tall. Derfor er det nok å løse ett av systemene (når man vurderer eksempler på denne måten, vil løsningen til ett system bli gitt). Metode 2: Anvendelse av metoden for å introdusere en ny variabel. I dette tilfellet introduseres notasjonen │x│= a, der a ≥ 0. Denne metoden mindre voluminøs i design.
Eksempler: №1 . Løs ligningen: 3x 2 – 4│x│= - 1 La oss bruke introduksjonen av en ny variabel. La oss betegne │x│= a, hvor a ≥ 0. Vi får ligningen 3a 2 - 4a + 1 = 0 D = 16 – 12 = 4 a 1 = 1 a 2 = 1 / 3 Gå tilbake til den opprinnelige variabelen: │ x│=1 og │х│= 1/3. Hver ligning har to røtter. Svar: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Løs ligningen: 5x 2 + 3│x│- 1 = 1 / 2 │x│ + 3x 2

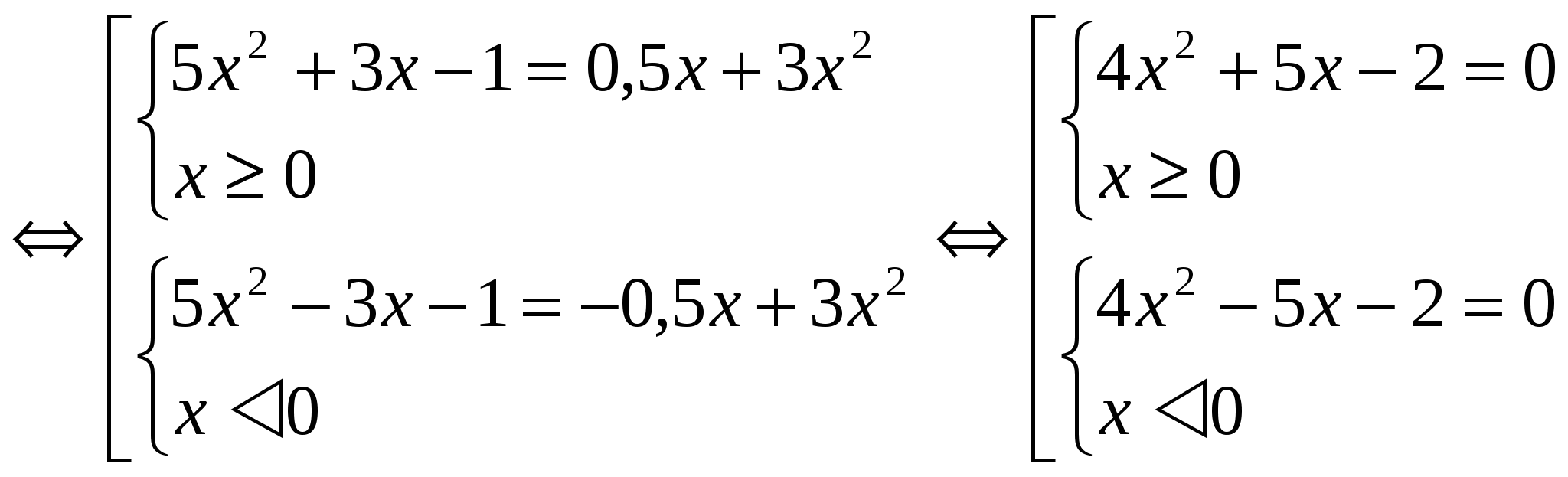La oss finne løsningen på det første systemet i populasjonen: 4x 2 + 5x – 2 =0 D = 57 x 1 = -5+√57 / 8 x 2 = -5-√57 / 8 Merk at x 2 ikke tilfredsstiller betingelsen x ≥ 0. Løsning det andre systemet vil være tallet motsatt av verdien x 1. Svar: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Løs ligningen: x 4 – │х│= 0 La oss betegne │х│= a, hvor a ≥ 0. Vi får ligningen a 4 – a = 0 a · (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Gå tilbake til den opprinnelige variabelen: │х│=0 og │х│= 1 x = 0; ± 1 Svar: x 1 = 0; X 2 = 1; X 3 = - 1.
Øvelser: №6. Løs ligningen: 2│х│ - 4,5 = 5 – 3 / 8 │х│ №7 . Løs ligningen, angi antall røtter i svaret ditt: 3x 2 - 7│x│ + 2 = 0 №8 . Løs ligningen, angi heltallsløsninger i svaret ditt: x 4 + │x│ - 2 = 0

Del 3. Ligninger av formen │F(x)│ = G(x)

Høyresiden av en ligning av denne typen avhenger av en variabel og har derfor en løsning hvis og bare hvis høyresiden er en funksjon G(x) ≥ 0. Den opprinnelige ligningen kan løses på to måter : 1 vei: Standard, basert på avsløringen av en modul basert på dens definisjon og består av en ekvivalent overgang til en kombinasjon av to systemer. │ F(x)│ =G(X)

Denne metoden kan rasjonelt brukes når det gjelder et komplekst uttrykk for funksjonen G(x) og et mindre komplekst for funksjonen F(x), siden det antas at ulikheter med funksjonen F(x) vil løses. Metode 2: Består i overgangen til et ekvivalent system der en betingelse er pålagt på høyre side. │ F(x)│= G(x)

Denne metoden er mer praktisk å bruke hvis uttrykket for funksjonen G(x) er mindre komplekst enn for funksjonen F(x), siden løsningen på ulikheten G(x) ≥ 0 antas i tillegg av flere moduler, anbefales det å bruke det andre alternativet. Eksempler: №1. Løs ligningen: │x + 2│= 6 -2x

(en vei) Svar: x = 1 1 / 3 №2.
│x 2 – 2x - 1│= 2 (x + 1)

(2-veis) Svar: Produktet av røttene er 3.
№3. Løs ligningen og angi summen av røttene i svaret ditt:
│x - 6│= x 2 - 5x + 9

Svar: summen av røttene er 4.
Øvelser: №9. │x + 4│= - 3x №10. Løs ligningen, angi antall løsninger i svaret:│x 2 + x - 1│= 2x – 1 №11 . Løs ligningen, angi produktet av røttene i svaret ditt:│x + 3│= x 2 + x – 6

Del 4. Ligninger av formen │F(x)│= F(x) og │F(x)│= - F(x)

Ligninger av denne typen kalles noen ganger "de vakreste." Siden høyre side av ligningene avhenger av variabelen, eksisterer løsninger hvis og bare hvis høyre side er ikke-negativ. Derfor er de opprinnelige ligningene ekvivalente med ulikhetene:
│F(x)│= F(x) F(x) ≥ 0 og │F(x)│= - F(x) F(x) Eksempler: №1 . Løs ligningen, angi den minste heltallsroten i svaret ditt: │5x - 3│= 5x – 3 5x – 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Svar: x = 1№2. Løs ligningen, angi lengden på intervallet i svaret ditt: │х 2 - 9│= 9 – x 2 x 2 – 9 ≤ 0 (x – 3) (x + 3) ≤ 0 [- 3; 3] Svar: lengden på gapet er 6.№3 . Løs likningen og angi antall heltallsløsninger i svaret ditt: │2 + x – x 2 │= 2 + x – x 2 2 + x – x 2 ≥ 0 x 2 – x – 2 ≤ 0 [- 1; 2] Svar: 4 hele løsninger.№4 . Løs ligningen og angi den største roten i svaret ditt:
│4 – x –

│= 4 – x –

x 2 – 5x + 5 = 0 D = 5 x 1,2 =

≈ 1,4

Svar: x = 3.

Øvelser: №12. Løs ligningen, angi hele roten i svaret ditt: │x 2 + 6x + 8│= x 2 + 6x + 8 №13. Løs ligningen, angi antall heltallsløsninger i svaret ditt: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Løs ligningen i svaret ditt, angi et heltall som ikke er roten til ligningen:

Del 5. Ligninger av formen │F(x)│= │G(x)│

Siden begge sider av ligningen er ikke-negative, innebærer løsningen å vurdere to tilfeller: submodulære uttrykk er like eller motsatte i fortegn. Derfor er den opprinnelige ligningen ekvivalent med kombinasjonen av to ligninger: │ F(x)│= │ G(x)│

Eksempler: №1. Løs ligningen, angi hele roten i svaret ditt: │x + 3│=│2x - 1│

Svar: hel rot x = 4.№2. Løs ligningen: │ x – x 2 - 1│=│2x – 3 – x 2 │

Svar: x = 2.№3 . Løs ligningen og angi produktet av røttene i svaret ditt:

Rotligninger 4x 2 + 2x – 1 = 0 x 1,2 = - 1±√5 / 4 Svar: produktet av røttene er – 0,25. Øvelser: №15 . Løs ligningen og angi hele løsningen i svaret ditt: │x 2 – 3x + 2│= │x 2 + 6x - 1│ №16. Løs ligningen, angi den minste roten i svaret:│5x - 3│=│7 - x│ №17 . Løs ligningen og angi summen av røttene i svaret ditt:

Del 6. Eksempler på løsning av ikke-standardiserte ligninger

I denne delen vil vi se på eksempler på ikke-standardiserte ligninger, når vi løser hvilke absoluttverdien av uttrykket avsløres per definisjon. Eksempler:

№1. Løs ligningen, angi summen av røttene i svaret ditt: x · │x│- 5x – 6 = 0
Svar: summen av røttene er 1 №2. . Løs ligningen, angi den minste roten i svaret: x 2 - 4x ·
- 5 = 0
Svar: mindre rot x = - 5. №3. Løs ligningen:

Svar: x = -1. Øvelser: №18. Løs ligningen og angi summen av røttene: x · │3x + 5│= 3x 2 + 4x + 3
№19. Løs ligningen: x 2 – 3x =

№20. Løs ligningen:

Del 7. Ligninger av formen │F(x)│+│G(x)│=0

Det er lett å legge merke til at på venstre side av ligningen av denne typen er summen av ikke-negative størrelser. Derfor har den opprinnelige ligningen en løsning hvis og bare hvis begge leddene er lik null på samme tid. Ligningen er ekvivalent med ligningssystemet: │ F(x)│+│ G(x)│=0
Eksempler: №1 . Løs ligningen:

Svar: x = 2. №2. Løs ligningen: Svar: x = 1. Øvelser: №21. Løs ligningen: №22 . Løs ligningen og angi summen av røttene i svaret ditt: №23 . Løs ligningen og angi antall løsninger i svaret ditt:

Del 8. Ligninger av formen │a 1 x + b 1 │±│a 2 x + b 2 │± … │a n x +b n │= m

For å løse likninger av denne typen brukes intervallmetoden. Hvis vi løser det ved sekvensiell utvidelse av moduler, får vi n sett med systemer, noe som er veldig tungvint og upraktisk. La oss vurdere intervallmetodealgoritmen: 1). Finn variabelverdier X, der hver modul er lik null (null av submodulære uttrykk):

2). Merk de funnet verdiene på en talllinje, som er delt inn i intervaller (antall intervaller er henholdsvis lik n+1 ) 3). Bestem med hvilket fortegn hver modul avsløres ved hvert av de oppnådde intervallene (når du lager en løsning, kan du bruke en talllinje, markere tegnene på den) 4). Den opprinnelige ligningen tilsvarer aggregatet n+1 systemer, hvor variabelens medlemskap er angitt X ett av intervallene. Eksempler: №1 . Løs ligningen og angi den største roten i svaret ditt:

1). La oss finne nullpunktene til de submodulære uttrykkene: x = 2; x = -3 2). La oss merke de funnet verdiene på talllinjen og bestemme med hvilket tegn hver modul blir avslørt på de resulterende intervallene:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)

- ingen løsninger Ligningen har to røtter. Svar: den største roten x = 2. №2. Løs ligningen og oppgi hele roten i svaret ditt:

1). La oss finne nullpunktene til de submodulære uttrykkene: x = 1,5; x = - 1 2). La oss merke de funnet verdiene på talllinjen og bestemme med hvilket tegn hver modul blir avslørt på de resulterende intervallene: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x – 3 2x – 3 2x – 3 - - +
3).

Det siste systemet har ingen løsninger, derfor har ligningen to røtter. Når du løser ligningen, bør du være oppmerksom på "-"-tegnet foran den andre modulen. Svar: hel rot x = 7. №3. Løs ligningen, angi summen av røttene i svaret ditt: 1). La oss finne nullpunktene til de submodulære uttrykkene: x = 5; x = 1; x = - 2 2). La oss merke de funnet verdiene på talllinjen og bestemme med hvilket tegn hver modul blir avslørt ved de resulterende intervallene: x – 5 x – 5 x – 5 x – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).

Ligningen har to røtter x = 0 og 2. Svar: summen av røttene er 2. №4 . Løs ligningen: 1). La oss finne nullpunktene til de submodulære uttrykkene: x = 1; x = 2; x = 3,2). La oss bestemme med hvilket tegn hver modul blir avslørt på de resulterende intervallene. 3).

La oss kombinere løsningene til de tre første systemene. Svar: ; x = 5.
Øvelser: №24. Løs ligningen:

№25. Løs ligningen og angi summen av røttene i svaret ditt: №26. Løs ligningen og angi den minste roten i svaret ditt: №27. Løs ligningen og angi den største roten i svaret ditt:

Seksjon 9. Ligninger som inneholder flere moduler

Ligninger som inneholder flere moduler antar tilstedeværelsen av absolutte verdier i submodulære uttrykk. Det grunnleggende prinsippet for å løse ligninger av denne typen er sekvensiell avsløring av moduler, som starter med den "eksterne". Under løsningen brukes teknikkene omtalt i avsnitt nr. 1, nr. 3.

Eksempler: №1. Løs ligningen:
Svar: x = 1; - elleve. №2. Løs ligningen:
Svar: x = 0; 4; - 4. №3. Løs ligningen og angi produktet av røttene i svaret ditt:
Svar: produktet av røttene er – 8. №4. Løs ligningen:
La oss betegne populasjonsligningene (1) Og (2) og vurder løsningen til hver av dem separat for enkel design. Siden begge ligningene inneholder mer enn én modul, er det mer praktisk å utføre en ekvivalent overgang til sett med systemer. (1)

(2)

Svar:
Øvelser: №36. Løs ligningen, angi summen av røttene i svaret ditt: 5 │3x-5│ = 25 x №37. Løs ligningen, hvis det er mer enn én rot, angi summen av røttene i svaret ditt: │x + 2│ x – 3x – 10 = 1 №38. Løs ligningen: 3 │2х -4│ = 9 │х│ №39. Løs ligningen og angi antall røtter i svaret ditt: 2 │ sin x│ = √2 №40 . Løs ligningen og angi antall røtter i svaret ditt:

Del 3. Logaritmiske ligninger.

Før du løser de følgende ligningene, er det nødvendig å gjennomgå egenskapene til logaritmer og logaritmisk funksjon. Eksempler: №1. Løs ligningen, angi produktet av røttene i svaret ditt: log 2 (x+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

Tilfelle 1: hvis x ≥ - 1, så log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – tilfredsstiller betingelsen x ≥ - 1 2 tilfelle: hvis x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – tilfredsstiller tilstand x - 1
Svar: produktet av røttene er – 15.
№2. Løs ligningen, angi summen av røttene i svaret ditt: lg
O.D.Z.

Svar: summen av røttene er 0,5.
№3. Løs ligningen: log 5
O.D.Z.

Svar: x = 9. №4. Løs ligningen: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 La oss bruke formelen for å flytte til en annen base. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 La oss finne nullene til de submodulære uttrykkene: x = 25; x = Disse tallene deler arealet akseptable verdier i tre intervaller, så ligningen tilsvarer et sett med tre systemer.
Svar: )

hjem » Bygningselementer og strukturer » Kvadratisk ligning modulo hvordan løses. Hvordan løse likninger med modul